Begriffsklärung
Die Standardabweichung gibt an, wie stark die Werte einer Datenmenge im Durchschnitt von ihrem Mittelwert abweichen. • Eine kleine Standardabweichung bedeutet, dass die Werte nah am Mittelwert liegen (geringe Streuung). • Eine große Standardabweichung bedeutet, dass die Werte weit gestreut sind (hohe Streuung). Die Standardabweichung wird oft mit σ (Sigma) bezeichnet.
Wie wird die Standardabweichung berechnet?
Es gibt zwei verschiedene Formeln – je nachdem, ob du eine Grundgesamtheit oder eine Stichprobe betrachtest.
A. Standardabweichung der Grundgesamtheit (σ)
Wenn du alle Werte einer Population hast, verwendest du die Formel: 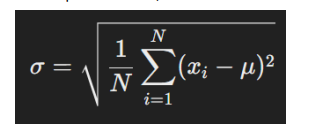
Bedeutung der Symbole:
• x|i= einzelner Wert in der Datenmenge
• μ = Mittelwert der gesamten Population
• N = Anzahl der Werte in der Population
• σ = Standardabweichung
B. Standardabweichung einer Stichprobe (s)
Wenn du nur eine Stichprobe (Teilmenge) der gesamten Population hast, verwendest du:
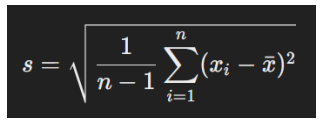
Der einzige Unterschied: Wir teilen durch n−1 statt durch N, um Verzerrungen bei kleinen Stichproben zu vermeiden.
Bedeutung der Symbole:
• = Stichprobenmittelwert
• n = Anzahl der Werte in der Stichprobe
• s = Stichproben-Standardabweichung
Beispielrechnung
Angenommen, du hast die Werte: 4, 7, 10, 6, 8
Schritt 1: Mittelwert berechnen
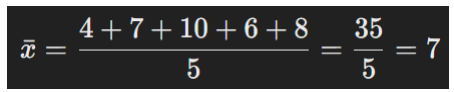
Schritt 2: Abweichungen vom Mittelwert quadrieren
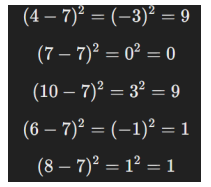
Schritt 3: Durchschnitt der quadrierten Abweichungen berechnen
(bei einer Population würden wir durch N = 5 teilen, aber wir nehmen eine Stichprobe, also n−1=4 ):

Also beträgt die Standardabweichung ca. 2.24.
Interpretation der Standardabweichung
• Wenn die Standardabweichung klein ist, liegen die Daten nah am Mittelwert.
• Wenn die Standardabweichung groß ist, sind die Daten weiter verstreut.
• In einer Normalverteilung gilt:
o 68 % der Werte liegen innerhalb einer Standardabweichung vom Mittelwert
o 95 % innerhalb von zwei Standardabweichungen
o 99,7 % innerhalb von drei Standardabweichungen
Fazit
• Die Standardabweichung misst, wie weit die Daten vom Mittelwert abweichen
• Sie hilft dabei, die Streuung einer Datenmenge zu verstehen.
• Wird häufig in Statistik, Wirtschaft und Naturwissenschaften verwendet.