Baumdiagramme

Baumdiagramme kommen häufig im Bereich der Stochastik zur Anwendung. Sie sind hilfreich beim Darstellen eines Zufallsexperimentes.

Das ist ein Beispiel für ein allgemeines Baumdiagramm:

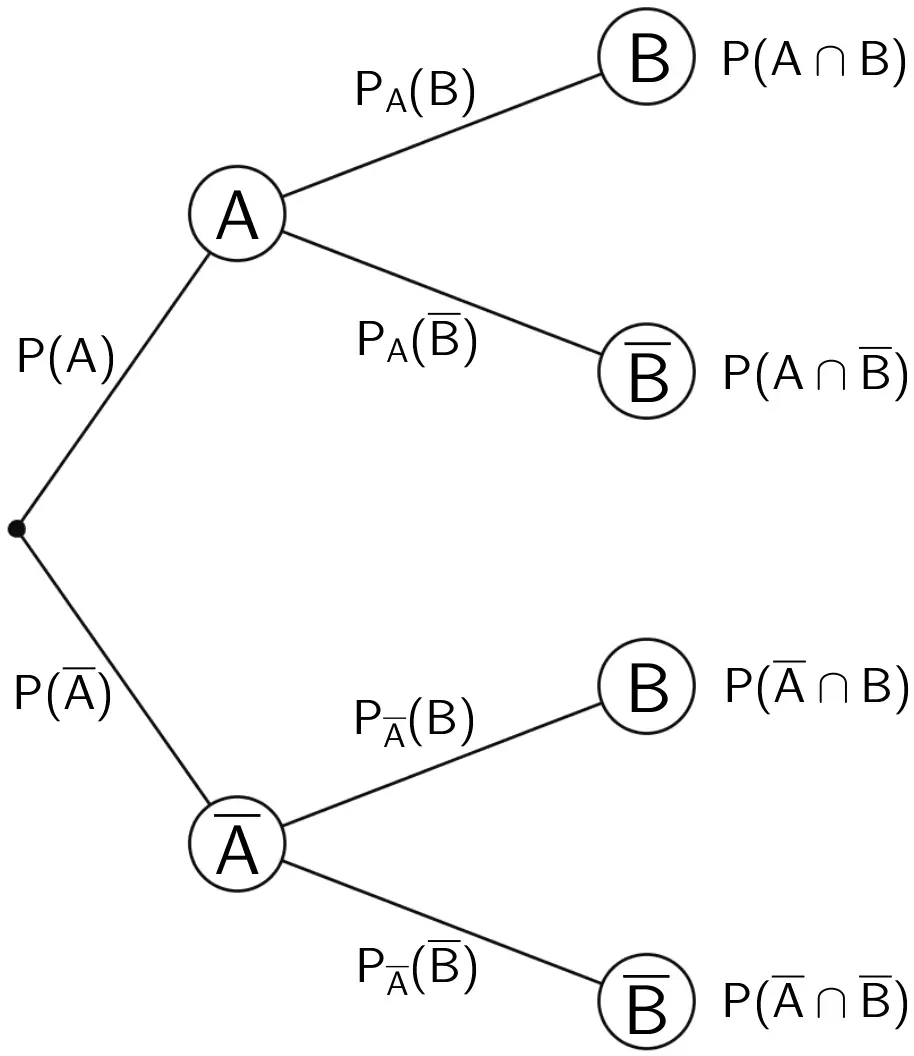
Diese können sehr hilfreich sein, um einen Überblick über ein Zufallsexperiment zu erhalten.

1. Pfadregel: Produktregel

Mithilfe der Produktregel kann die Wahrscheinlichkeit dafür berechnet werden, dass ein bestimmtes Ereignis eintritt.

Hier z. B.: Erst tritt A ein und dann B:

P (A) \cdot P_{A} (B) = P (A \cap B)

2. Pfadregel: Summenregel

Mithilfe der Summenregel kann die Wahrscheinlichkeit dafür berechnet werden, dass ein Ereignis im hinteren Teil des Baumes überhaupt eintritt. Hierfür Multipliziert man entlang der Pfade

Hier z. B.: Die Wahrscheinlichkeit, dass Ereignis B eintritt:

P (B) = P (A \cap B) + P (\overline{A} \cap B)

Weiteres Beispiel: $\overline{B}$ Tritt ein:

P (\overline{B}) = P (A \cap \overline{B}) + P (\cap \overline{A} \cap \overline{B})

Mathematische Bedeutung

Mit Hilfe eines Baumdiagramms lassen sich folglich mehrstufige Zufallsexperimente übersichtlich darstellen. Die Wahrscheinlichkeiten für verschiedene Ergebnisse lassen sich so einfach berechnen. Durch Ergänzung der Zweigwahrscheinlichkeiten an den einzelnen Ästen werden diese zu sogenannten Wahrscheinlichkeitsbäumen. Die einzelnen Wahrscheinlichkeiten werden dabei für gewöhnlich als Dezimalbrüche angegeben. Anschließend kann man die Wahrscheinlichkeiten für verschiedene Ergebnisausgänge ganz einfach berechnen.

Beispiel zu Baumdiagrammen

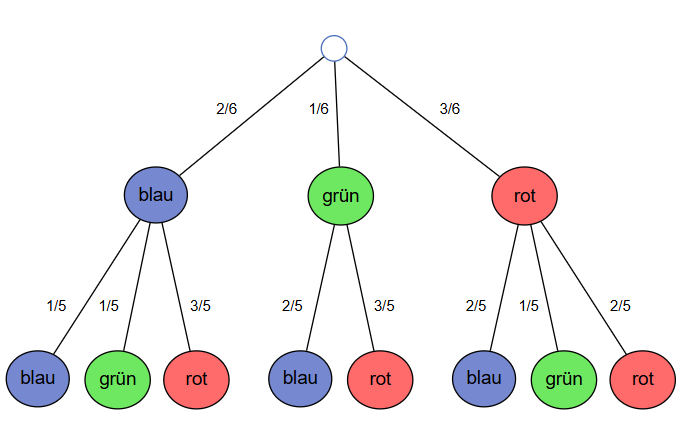
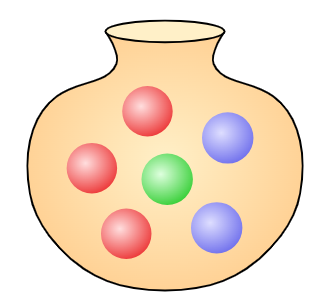
In einer Urne befinden sich drei rote, zwei blaue und eine grüne Kugel, also insgesamt 6 Kugeln. Es wird zweimal eine Kugel (ohne zurücklegen) gezogen und ihre Farbe notiert.

Aufgabe: Zeichne ein vollständiges Baumdiagramm (mit Pfadwahrscheinlichkeiten).

Schritt 1: Anzahl der Stufen festlegen.

Schritt 2: Die möglichen Ereignisse verfassen (In dem Fall: rot, blau, grün)

Schritt 3: Warscheinlichkeiten für die erste Stufe aufstellen. Man teilt die Anzahl der Kugeln einer Farbe durch die Gesamtanzahl an Kugeln

Schritt 4: Wahrscheinlichkeiten für die zweite Stufe aufstellen. Achtung: Da es ohne Zurücklegen ist, gibt es nur noch 5 Kugeln.

Schritt 5: Man teilt die nach der 1.Stufe vorhandene Anzahl der Kugeln einer Farbe durch die Gesamtanzahl an Kugeln die übrig bleibt.